Prof. Peng Zhang: Variational Quantum Universal Eigensolver
Introduction
 |
| Professor Peng Zhang |
In a remarkable advancement within the field of quantum computing, Prof. Peng Zhang has pioneered the Universal Variational Quantum Eigensolver (VQUE) for Non-Hermitian Systems. Traditionally, quantum algorithms have focused on Hermitian matrices, which are well-suited to the capabilities of quantum computers. However, the VQUE algorithm breaks new ground by extending these capabilities to the domain of non-Hermitian matrices.
Non-Hermitian matrices are prevalent in various scientific and engineering disciplines, notably in the analysis of power systems, where they play a critical role in understanding system dynamics and stability. The VQUE algorithm extending its utility to a wider range of problems. This development contributes to the evolving landscape of quantum algorithms, offering new opportunities for practical applications.
Variational Quantum Universal Eigensolver (VQUE)
VQUE is an innovative algorithm that is uniquely capable of computing the eigenvalues of non-Hermitian matrices. It leverages the foundational principles of Schur’s triangularization theory, traditionally a classical mathematical method, and adapts it to the quantum context. This adaptation allows VQUE to handle non-unitary matrices, which has been a significant challenge for quantum algorithms. A notable aspect of VQUE is its compatibility with noisy intermediate-scale quantum (NISQ) computers, making it a versatile tool for current quantum computing platforms.
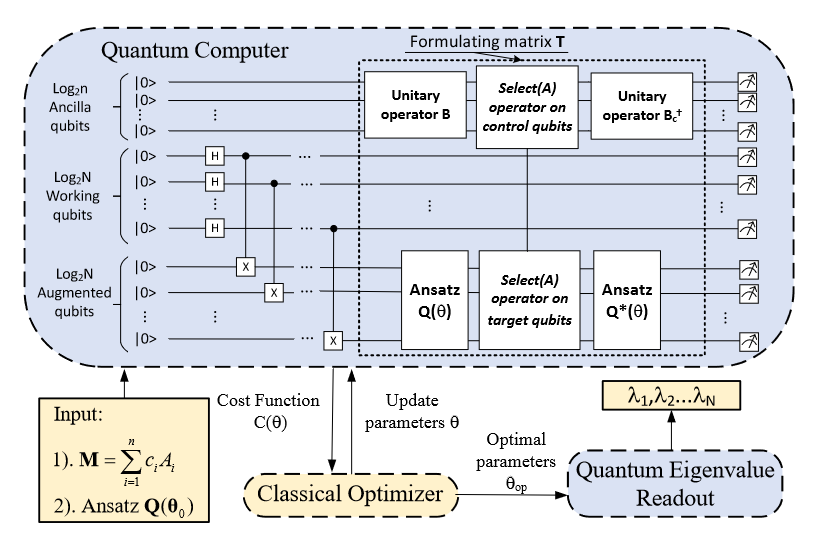
Schematic diagram of Variational quantum universal eigensolver (VQUE)
Quantum Process Snapshot Technique
One of the key innovations in VQUE is the Quantum Process Snapshot technique. This method is pivotal in ensuring that VQUE maintains the computational advantages of quantum algorithms. It efficiently checks whether a unitary operator is triangular, a crucial step in the algorithm, with the addition of only a few quantum gates. This efficiency is vital in preserving the speed and power that quantum computing brings to the eigensolver problem.
Real-World Applications and Challenges
The real-world applicability of VQUE has been demonstrated through its successful deployment on an actual quantum computer. This practical application is a critical test of the algorithm’s feasibility and effectiveness. In addition, extensive parametric studies have been conducted to assess the scalability and performance of VQUE across different scenarios and applications. These studies are essential in understanding the range and limits of VQUE's capabilities.
The research also brings to light several challenges that need to be addressed for the wider adoption of VQUE. One of the primary challenges is the need for efficient methods to decompose non-Hermitian matrices into a form suitable for quantum computing. Additionally, optimizing the algorithm for specific applications and managing the computational demands, especially in large-scale problems, remain areas of ongoing research and development.
Conclusion
In conclusion, the development of the Universal Variational Quantum Eigensolver is a noteworthy achievement in the field of quantum computing. It opens up new possibilities for solving complex problems that involve non-Hermitian matrices, a task that was previously out of reach for quantum algorithms.